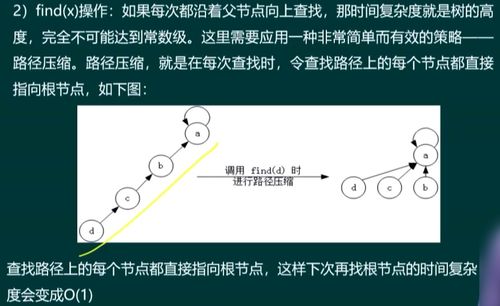
浙江大學2005年計算機研究生復試上機考試中的“暢通工程”問題,是一個經典的圖論與數據結構應用題,其核心考察點在于并查集(Union-Find)算法。題目通常描述為:給定若干城鎮及它們之間的道路連接情況,要求計算至少還需要修建多少條道路,才能使所有城鎮實現交通暢通。這本質上是一個求解連通分量個數的問題。
并查集是一種用于處理不相交集合合并與查詢的高效數據結構,其兩大核心操作“查找”與“合并”,恰恰對應了網絡工程中設備連通性判斷與網絡整合的核心需求。在“暢通工程”問題中,每個城鎮初始時被視為一個獨立的集合(即一個連通分量)。每讀入一條已存在的道路,就意味著連接了兩個城鎮,需要對它們所屬的集合進行合并操作。所有直接或間接相連的城鎮都會歸屬到同一個集合中。統計最終剩余獨立集合的個數減一,即為需要新增道路的最小數量。
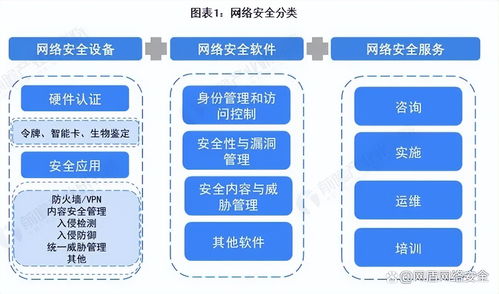
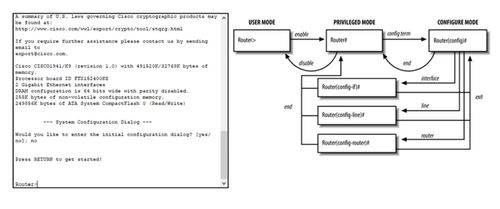
這種算法思想與計算機網絡工程中的網絡構建與故障診斷有著深刻的共鳴。例如,在規劃一個大型企業網絡或數據中心網絡時,網絡工程師需要確保所有關鍵節點(如服務器、交換機、路由器)在物理或邏輯上是連通的,以保證服務的可達性。可以將每個網絡設備視為一個節點,設備間的物理鏈路或配置好的通信通道視為邊。利用并查集的思想,可以快速判斷網絡是否全連通,或者定位出導致網絡分割的故障鏈路——這類似于找出哪些“道路”缺失導致了“城鎮”隔離。
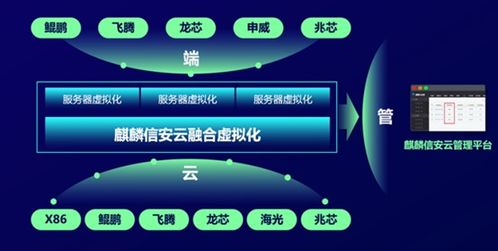
更進一步,在現代軟件定義網絡和虛擬網絡功能部署中,并查集的變體或思想可用于動態管理網絡資源的歸屬與策略應用域。當需要將一組網絡設備劃分到同一個虛擬網絡或安全域時,合并操作就對應著策略的統一應用;查找操作則用于快速判定某個數據流或設備是否屬于某個受控域,從而決定數據轉發路徑或安全策略。
因此,浙大這道復試題目不僅考察了學生對基礎數據結構的掌握和編碼能力,更隱喻了計算機科學基礎理論與大型工程實踐(尤其是網絡工程)之間的緊密聯系。它提醒未來的計算機和網絡工程師,許多復雜的系統性問題,其底層可能依賴于簡潔而強大的抽象模型與算法。從求解“暢通工程”的并查集代碼,到設計一個健壯、可擴展的全球性計算機網絡,其中貫穿的核心思想之一,正是對“連通性”這一基本屬性的高效管理與優化。